(·湖北鄂州,19题,8分)八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
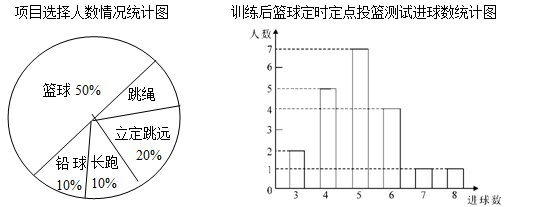
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.