(1)小明说:“请你任意想一个数,把这个数乘2后加8,然后除以4,再减去你原来所想的那个数的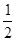 ,我可以知道你计算的结果是2.”
,我可以知道你计算的结果是2.”
请你帮助小明说明上述结论的正确性.
如果设任意想的那个数为x,则根据题意,得代数式(请完善下面的解题过程):
(2)在(1)中,得到的代数式化简后结果为2,它不含有x,我们称之为“与x无关”.
试解决下列“无关”类问题:
①多项式(2x+4yx-1)-2(x+2xy)的值()
| A.仅与x的大小无关 |
B.仅与y的大小无关 |
| C.与x、y的大小都无关 |
D.与x、y的大小都有关 |
②如果已知代数式 的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?
的值与其中某个字母的取值无关,你能求出哪一个字母的值?此时这个字母的值是多少?