某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: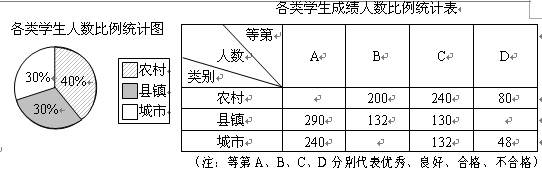
(1)请将上面表格中缺少的三个数据补充完整
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
相关知识点
推荐套卷
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
(1)请将上面表格中缺少的三个数据补充完整
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.