已知函数
的图像(如图所示)过点
、
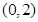和点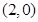
，且函数图像关于点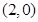对称;直线
和
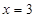及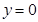
是它的渐近线.现要求根据给出的函数图像研究函数
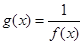的相关性质与图像,
(1)写出函数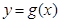
的定义域、值域及单调递增区间;
（2）作函数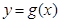的大致图像（要充分反映由图像及条件给出的信息）;
（3）试写出的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
相关试题
,是否存在斜率为k(k≠0)的直线
,使
的垂直平分线经过点M（0,－1），求斜率k的取值范围.
，与直线x+y－1=0相交于两点Ｍ、Ｎ，且以
为直径的圆经过坐标原点．求椭圆的方程．
,动点
在双曲线
上运动,且
,求点P的轨迹方程.
的焦点F作倾斜角为
的直线交抛物线于A、B两点，若线段AB的长为8，求此抛物线的方程.
与双曲线
有且仅有一个公共点,求实数
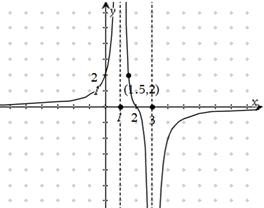
的值.推荐套卷
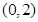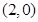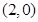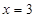已知函数的图像(如图所示)过点、和点，且函数图像关于点对称;直线和及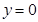是它的渐近线.现要求根据给出的函数图像研究函数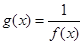的相关性质与图像,
(1)写出函数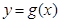的定义域、值域及单调递增区间;
（2）作函数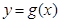的大致图像（要充分反映由图像及条件给出的信息）;
（3）试写出的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
粤公网安备 44130202000953号