如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.
⑴求证:△ACD≌△BCE; 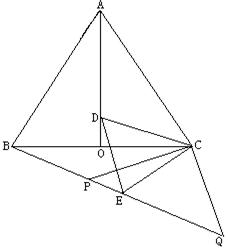 ⑵延长BE至Q,P为BQ上一点,连结CP、CQ使CP=CQ=5,若PQ=6时,求AO的长.
⑵延长BE至Q,P为BQ上一点,连结CP、CQ使CP=CQ=5,若PQ=6时,求AO的长.
相关知识点
推荐套卷
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.
⑴求证:△ACD≌△BCE;  ⑵延长BE至Q,P为BQ上一点,连结CP、CQ使CP=CQ=5,若PQ=6时,求AO的长.
⑵延长BE至Q,P为BQ上一点,连结CP、CQ使CP=CQ=5,若PQ=6时,求AO的长.