．（本小题满分10分）选修4－1：几何证明选讲
已知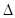
ABC中，AB=AC, D是 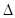ABC外接圆劣弧AC弧上的点（不与点A,C重合），延长BD至E。
（1）求证：AD的延长线平分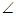
CDE；
（2）若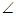BAC=30°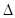，ABC中BC边上的高为2+
，
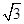求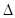ABC外接圆的面积。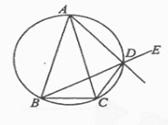 
；
，其中
的顶点
，
边上的中线
所在的直线方程为
，
边上的高
所在直线方程为
．
的坐标；
的方程．
经过点
和直线
相切，且圆心在直线
上，求圆
和
的交点，且垂直于直线
的直线方程．
，求值：
推荐套卷
．（本小题满分10分）选修4－1：几何证明选讲
已知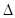ABC中，AB=AC, D是 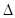ABC外接圆劣弧AC弧上的点（不与点A,C重合），延长BD至E。
（1）求证：AD的延长线平分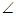CDE；
（2）若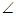BAC=30°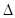，ABC中BC边上的高为2+，
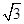求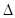ABC外接圆的面积。
粤公网安备 44130202000953号