某高中采取分层抽样的方法从应届高二学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
| 性别 科目 |
男 |
女 |
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的男生和报考理科的女生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关? (参考公式和数据:χ2 (其中
(其中 ))
))
相关知识点
推荐套卷
 是奇函数(其中
是奇函数(其中 ).
). 的值;
的值;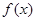 在
在 上的单调性并证明;
上的单调性并证明;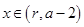 时,
时, ,求
,求 与
与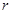 的值.
的值.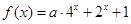 ,其中
,其中 .
. ,若当
,若当 时,
时, 有意义,求
有意义,求 的取值范围;
的取值范围; ,使得关于
,使得关于 的方程
的方程 对于任意非正实数
对于任意非正实数
 ,当
,当 时,函数取最小值
时,函数取最小值 ,且
,且 .
. 的解析式;
的解析式; 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围.
的取值范围. ,集合
,集合 .
. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号