（本小题满分12分）
某市场搞国庆促销活动,一个人同时转动如图2所示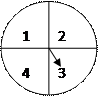
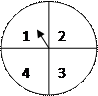的两个转盘，记转盘（甲）得到的数
，转盘（乙）
得到的数为
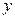，设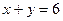
为中一等奖、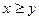
为中二等奖．
（Ⅰ）求中一等奖的概率； （甲） 图2 （乙）
（Ⅱ）求中二等奖的概率．
．
行里的最后一个数字是多少？
对一切正整数
都成立，那么
的值为多少？
．
中，
，
，
，试猜想这个数列的通项公式．推荐套卷
（本小题满分12分）
某市场搞国庆促销活动,一个人同时转动如图2所示的两个转盘，记转盘（甲）得到的数，转盘（乙）
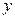得到的数为，设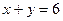为中一等奖、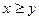
为中二等奖．
（Ⅰ）求中一等奖的概率； （甲） 图2 （乙）
（Ⅱ）求中二等奖的概率．
粤公网安备 44130202000953号