如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA ⊥平面ABCD,AP=AB=2,BC=2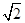 
，E，F分别是AD，PC的中点
（Ⅰ）证明：PC ⊥平面BEF；（Ⅱ）求平面BEF与平面BAP夹角的大小。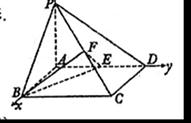
相关试题
=3a，
=2b，求
，．
，且
，试求t关于k的函数。
ABCD的两条对角线AC与BD交于E，O是任意一点，
+
+
+
=4
推荐套卷
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA ⊥平面ABCD,AP=AB=2,BC=2 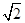，E，F分别是AD，PC的中点
（Ⅰ）证明：PC ⊥平面BEF；（Ⅱ）求平面BEF与平面BAP夹角的大小。
粤公网安备 44130202000953号