.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的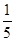 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: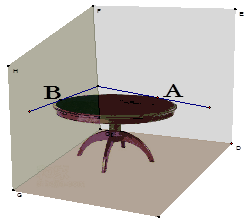 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
相关知识点
推荐套卷
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的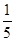 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.