设函数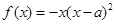 (
(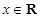 ),其中
),其中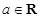 。
。
(Ⅰ)当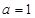 时,求曲线
时,求曲线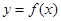 在点
在点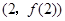 处的切线方程;
处的切线方程;
(Ⅱ)当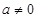 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当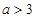 时,在区间
时,在区间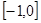 上是否存在实数
上是否存在实数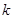 使不等式
使不等式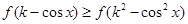 对任意的
对任意的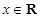 恒成立 , 若存在,求出
恒成立 , 若存在,求出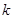 的值,若不存在,说明理由。
的值,若不存在,说明理由。
推荐套卷
设函数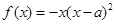 (
(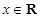 ),其中
),其中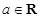 。
。
(Ⅰ)当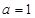 时,求曲线
时,求曲线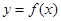 在点
在点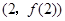 处的切线方程;
处的切线方程;
(Ⅱ)当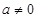 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当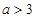 时,在区间
时,在区间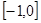 上是否存在实数
上是否存在实数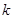 使不等式
使不等式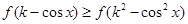 对任意的
对任意的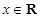 恒成立 , 若存在,求出
恒成立 , 若存在,求出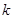 的值,若不存在,说明理由。
的值,若不存在,说明理由。