本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
若点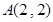 在矩阵
在矩阵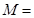
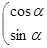
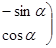 对应变换的作用下得到的点为
对应变换的作用下得到的点为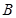
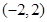 ,求矩阵
,求矩阵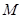 的逆矩阵.
的逆矩阵.
推荐套卷
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
若点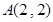 在矩阵
在矩阵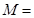
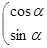
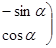 对应变换的作用下得到的点为
对应变换的作用下得到的点为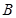
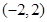 ,求矩阵
,求矩阵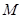 的逆矩阵.
的逆矩阵.