如图,在四棱锥P—ABCD中,底面ABCD是菱形,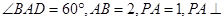 平面ABCD,E是PC的中点,F是AB的中点。
平面ABCD,E是PC的中点,F是AB的中点。
(1)求证:BE//平面PDF;
(2)求证:平面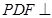 平面PAB;
平面PAB;
(3)求平面PAB与平面PCD所成的锐二面角的大小。
推荐套卷
如图,在四棱锥P—ABCD中,底面ABCD是菱形,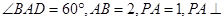 平面ABCD,E是PC的中点,F是AB的中点。
平面ABCD,E是PC的中点,F是AB的中点。
(1)求证:BE//平面PDF;
(2)求证:平面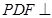 平面PAB;
平面PAB;
(3)求平面PAB与平面PCD所成的锐二面角的大小。