甲、乙、丙三人在同一办公室工作,办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为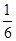 、
、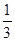 、
、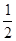 。若在同一时间内打进三个电话,且各个电话相互独立,求:
。若在同一时间内打进三个电话,且各个电话相互独立,求: 这三个电话是打给同一个人的概率;
这三个电话是打给同一个人的概率; 这三个电话中恰有两个是打给甲的概率。
这三个电话中恰有两个是打给甲的概率。
推荐套卷
甲、乙、丙三人在同一办公室工作,办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为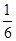 、
、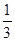 、
、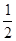 。若在同一时间内打进三个电话,且各个电话相互独立,求:
。若在同一时间内打进三个电话,且各个电话相互独立,求: 这三个电话是打给同一个人的概率;
这三个电话是打给同一个人的概率; 这三个电话中恰有两个是打给甲的概率。
这三个电话中恰有两个是打给甲的概率。