已知椭圆C：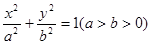
的两个焦点为
、
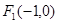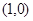，且经过点
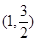，一组斜率为
的直线与椭圆C都相交于不同两点
、
。
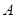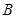（1）求椭圆C的方程；
（2）证明：线段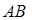
的中点都有在同一直线
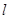上；
（3）对于（2）中的直线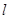，设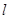与椭圆C交于两点M、N，试探究椭圆上使
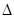MNQ面积为
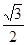的点Q有几个？证明你的结论。（不必具体求出Q点的坐标）
相关试题
中，角
所对的边分别为
，且
是方程
的两个根，且
，求：
的度数；
的长度。
；
的值；
的值；
，求证：
为纯虚数.
．
是纯虚数，求实数m的值；推荐套卷
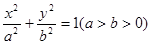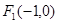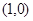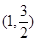已知椭圆C：的两个焦点为、，且经过点，一组斜率为的直线与椭圆C都相交于不同两点、。
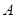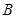（1）求椭圆C的方程；
（2）证明：线段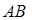的中点都有在同一直线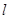上；
（3）对于（2）中的直线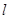，设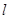与椭圆C交于两点M、N，试探究椭圆上使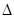MNQ面积为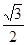的点Q有几个？证明你的结论。（不必具体求出Q点的坐标）
粤公网安备 44130202000953号