若⊙P与函数图象有且只有一个公共点,并且与 轴、
轴、 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.如图1,求
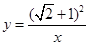 的伴圆的圆心P的坐标及半径r;
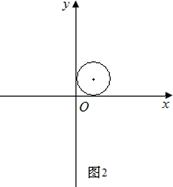
的伴圆的圆心P的坐标及半径r;如图2,⊙P的半径为1,若⊙P是二次函数
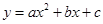 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;如图3,求一次函数
 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.

相关知识点
推荐套卷
若⊙P与函数图象有且只有一个公共点,并且与 轴、
轴、 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.如图1,求
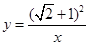 的伴圆的圆心P的坐标及半径r;
的伴圆的圆心P的坐标及半径r;如图2,⊙P的半径为1,若⊙P是二次函数
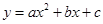 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;如图3,求一次函数
 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.

