(本小题满分16分)
对于函数
,若存在实数对(
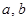),使得等式
对定义域中的每
一个
都成立,则称函数
是“(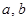)型函数”.
(1)判断函数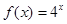
是否为“(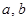)型函数”，并说明理由；
(2)已知函数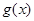
是“(1,4)型函数”, 当
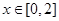时,都有
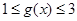成立,且当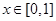
时,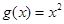
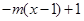
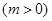,若,试求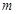
的取值范围.
x＋1的倾斜角的
，且分别满足下列条件的直线方程：(1)经过点(
，1＋
为空间四边形
的边
上的点，且
，求证：
.
中
，
面
，
，
面
.
推荐套卷
(本小题满分16分)
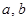对于函数,若存在实数对(),使得等式对定义域中的每
一个都成立,则称函数是“(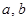)型函数”.
(1)判断函数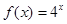是否为“(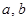)型函数”，并说明理由；
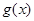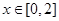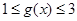(2)已知函数是“(1,4)型函数”, 当时,都有成立,且当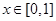
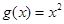
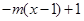
时,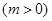,若,试求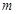的取值范围.
粤公网安备 44130202000953号