已知Rt△ABC的顶点坐标A（-3，0），直角顶点B（-1，-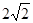
），顶点C在
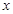轴上。
（1）求BC边所在直线的方程；
（2）圆M为Rt△ABC外接圆，其中M为圆心，求圆M的方程；
（3）直线
与Rt△ABC外接圆相切于第一象限，求切线与两坐标轴所围成的三角形面积最小时的切线方程。
中
，
求证：（1）对角线
⊥平面
。
的外心。
的中点。
（1）求直线
是异面直线，
求证：AD与BC是异面直线。
的三个顶点坐标为分别为：
试判断推荐套卷
已知Rt△ABC的顶点坐标A（-3，0），直角顶点B（-1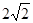，-），顶点C在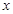轴上。
（1）求BC边所在直线的方程；
（2）圆M为Rt△ABC外接圆，其中M为圆心，求圆M的方程；
（3）直线与Rt△ABC外接圆相切于第一象限，求切线与两坐标轴所围成的三角形面积最小时的切线方程。
粤公网安备 44130202000953号