.将编号为1，2，3的三个小球随意放入编号为1，2，3的三个纸箱中，每个纸箱内有且只有一个小球，称此为一轮“放球”，设一轮“放球”后编号为i(i=1，2，3)的纸箱放入的小球编号为ai，定义吻合度误差为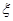
=|1－a1|+|2－a2|+|3－a3|。假设a1，a2，a3等可能地为1、2、3的各种排列，求⑴某人一轮“放球”满足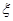=2时的概率。⑵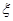的数学期望。
相关试题
,
，求
的值．
、
是关于
的二次方程
的两根，
，求
的范围。
的最大值为3，最小值为
．
的值；（2）当求
时，函数
的值域．
的周期为π,且图象上一个最低点为M（
，-2）．
］时，求f（x）的值域．
是关于
的方程
的两个实根，且
，求
的值推荐套卷
.将编号为1，2，3的三个小球随意放入编号为1，2，3的三个纸箱中，每个纸箱内有且只有一个小球，称此为一轮“放球”，设一轮“放球”后编号为i(i=1，2，3)的纸箱放入的小球编号为ai，定义吻合度误差为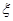=|1－a1|+|2－a2|+|3－a3|。假设a1，a2，a3等可能地为1、2、3的各种排列，求⑴某人一轮“放球”满足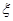=2时的概率。⑵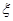的数学期望。
粤公网安备 44130202000953号