某城市计划在如图所示的空地 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕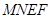 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 是边长为30米的正方形,电源在点
是边长为30米的正方形,电源在点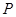 处,点
处,点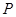 到边
到边 的距离分别为9米,3米,且
的距离分别为9米,3米,且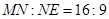 ,线段
,线段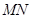 必过点
必过点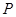 ,端点
,端点 分别在边
分别在边 上,设
上,设 米,液晶广告屏幕
米,液晶广告屏幕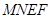 的面积为
的面积为 平方米.
平方米.
(Ⅰ)求 关于
关于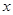 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)当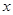 为何值时,液晶广告屏幕
为何值时,液晶广告屏幕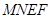 的面积
的面积 最小?
最小?
推荐套卷
某城市计划在如图所示的空地 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕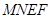 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 是边长为30米的正方形,电源在点
是边长为30米的正方形,电源在点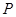 处,点
处,点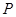 到边
到边 的距离分别为9米,3米,且
的距离分别为9米,3米,且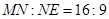 ,线段
,线段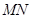 必过点
必过点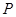 ,端点
,端点 分别在边
分别在边 上,设
上,设 米,液晶广告屏幕
米,液晶广告屏幕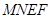 的面积为
的面积为 平方米.
平方米.
(Ⅰ)求 关于
关于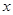 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)当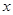 为何值时,液晶广告屏幕
为何值时,液晶广告屏幕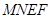 的面积
的面积 最小?
最小?