已知抛物线抛物线 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线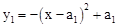 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为(,);
依此类推第n条抛物线yn的顶点坐标为(,);
所有抛物线的顶点坐标满足的函数关系是;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.