如图所示，椭圆C：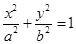
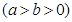的一个焦点为F(1,0)，且过点(2,0)
(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点，且直线AB垂直于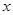
轴，又直线
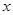：＝4与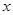轴交于点N，直线AF与BN交
于点M.
(ⅰ)求证：点M恒在椭圆C上；
(ⅱ)求△AMN面积的最大值．
轴切于点（5，0）并在
轴上截取弦长为10的圆的方程。
上任意一点P（ ），不等式
恒成立，求实数
的取值范围。
，直线
，点
是直线
上的一点，若
，求点
的轨迹方程．
，
，
，
为顶点的四边形是一个矩形．
，
，
，试判断
的形状，并给出证明．
推荐套卷
如图所示，椭圆C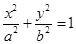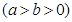：的一个焦点为F(1,0)，且过点(2,0)
(1)求椭圆C的方程;
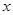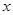(2)已知A、B为椭圆上的点，且直线AB垂直于轴，又直线：＝4与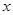轴交于点N，直线AF与BN交
于点M.
(ⅰ)求证：点M恒在椭圆C上；
(ⅱ)求△AMN面积的最大值．
粤公网安备 44130202000953号