如图示,四棱锥P----ABCD的底面是边长为1的正方形，PA^CD，PA = 1， PD =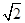 
,E为PD上一点，PE = 2ED.
(1) 求证：PA ^平面ABCD；
(2) 求二面角D---AC---E的正切值；
(3) 在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，
说明理由.
于A，
于B，如果PA=10，AB=6，求
,
，且
.
的取值的集合；
时, 
恒成立,求实数
的取值范围.
,
.
, 求
的值;
为坐标原点, 点
在第一象限, 求函数
的单调递增区间与值域.
中，
分别为角
的对边，
，
．
的值；
的值.推荐套卷
如图示,四棱锥P----ABCD的底面是边长为1的正方形，PA^CD，PA = 1， PD = 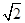,E为PD上一点，PE = 2ED.
(1) 求证：PA ^平面ABCD；
(2) 求二面角D---AC---E的正切值；
(3) 在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，
说明理由.
粤公网安备 44130202000953号