函数
的定义域关于原点对称，但不包括数0，对定义域中的任意实数
，在定义域中存在
使
，
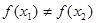，且满足以下3个条件。
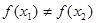（1）是定义域中的数，，则
（2）
，（
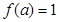是一个正的常数）
（3）当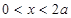
时，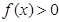
。
证明：（1）是奇函数；
（2）是周期函数，并求出其周期；
（3）在
内为减函数。
相关试题
是偶函数．
的值；
,若函数
与
的图象有且只有一个公共点，求实数
的取值范围．
是定义在
上的函数．
在
．
在区间
上有最大值
，求实数
的值．
．
时，求集合
；
，且
，求实数
的取值范围．
；
+
．相关知识点
推荐套卷
函数的定义域关于原点对称，但不包括数0，对定义域中的任意实数，在定义域中存在使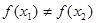，，且满足以下3个条件。
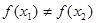（1）是定义域中的数，，则
（2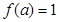），（是一个正的常数）
（3）当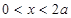时，。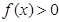
证明：（1）是奇函数；
（2）是周期函数，并求出其周期；
（3）在内为减函数。
粤公网安备 44130202000953号