已知在直角坐标平面XOY中，有一个不在Y轴上的动点P（x,y），到定点F（0，
）的距离比它到X轴的距离多，记P点的轨迹为曲线C
（I）求曲线C的方程；
（II）已知点M在Y轴上，且过点F的直线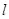
与曲线C交于A、B两点，若 
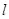为正三角形，求M点的坐标与直线的方程。
相关试题
，求
的值．
为锐角，
，求
的值．
的最大值为2，求实数a的值．
．
；
，若函数
在区间
上是增函数，求
的取值范围；
有解，求实数a的取值范围．
，若
的图象上相邻两条对称轴之间的距离为
，且当
时，函数
大值为1．
，且
，求
的值．推荐套卷
已知在直角坐标平面XOY中，有一个不在Y轴上的动点P（x,y），到定点F（0，）的距离比它到X轴的距离多，记P点的轨迹为曲线C
（I）求曲线C的方程；
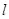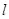（II）已知点M在Y轴上，且过点F的直线与曲线C交于A、B两点，若 为正三角形，求M点的坐标与直线的方程。
粤公网安备 44130202000953号