某企业生产A、B两种产品，生产每一吨产品所需的劳动力、煤和电耗如下表：
已知生产每吨A产品的利润是7万元，生产每吨B产品的利润是12万元，现因条件限制，该企业仅有劳动力300个，煤360吨，并且供电局只能供电200千瓦，试问该企业生产A、B两种产品各多少吨，才能获得最大利润？
| 产品品种 |
劳动力（个） |
煤（吨） |
电（千瓦） |
| A产品 |
3 |
9 |
4 |
| B产品 |
10 |
4 |
5 |
相关试题
(12分)如图，在四棱锥P-ABCD中，底面
ABCD是矩形,PA⊥平面ABCD，AP=AB，
BP=BC=2，E，F分别是PB,PC的中点.
(Ⅰ)证明：EF∥平面PAD；
(Ⅱ)求四棱锥E-ABCD的体积V；
(Ⅲ)求二面角E-AD-C的大小.
 |
,求
关于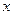
轴对称的直线方程；
，求过点
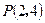与圆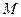
相切的切线方程
,求圆C关于原点对称的圆的方程；
,圆心在直线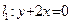
上,且与直线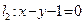
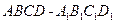．(Ⅰ)求证：平面
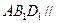平面
；
与
所成角的大小.
相关知识点
推荐套卷
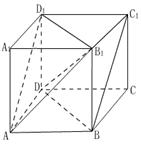
粤公网安备 44130202000953号