已知圆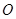 :
: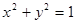 ,点
,点 在直线
在直线
 上,过点
上,过点 作圆
作圆 的两条切线,
的两条切线,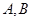 为两切点,
为两切点,
(1)求切线长 的最小值,并求此时点
的最小值,并求此时点 的坐标;
的坐标;
(2)点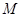 为直线
为直线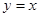 与直线
与直线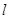 的交点,若在平面内存在定点
的交点,若在平面内存在定点 (不同于点
(不同于点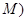 ,满足:对于圆
,满足:对于圆 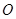 上任意一点
上任意一点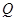 ,都有
,都有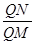 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点 的坐标;
的坐标;
(3)求 的最小值.
的最小值.
相关知识点
推荐套卷
已知圆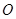 :
: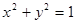 ,点
,点 在直线
在直线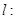
 上,过点
上,过点 作圆
作圆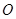 的两条切线,
的两条切线,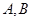 为两切点,
为两切点,
(1)求切线长 的最小值,并求此时点
的最小值,并求此时点 的坐标;
的坐标;
(2)点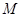 为直线
为直线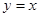 与直线
与直线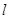 的交点,若在平面内存在定点
的交点,若在平面内存在定点 (不同于点
(不同于点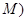 ,满足:对于圆
,满足:对于圆 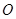 上任意一点
上任意一点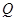 ,都有
,都有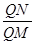 为一常数,求所有满足条件的点
为一常数,求所有满足条件的点 的坐标;
的坐标;
(3)求 的最小值.
的最小值.