已知二次函数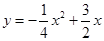 .
.(1)求它的对称轴与
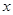 轴交点D的坐标;
轴交点D的坐标;(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为
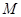 ,与
,与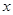 轴、
轴、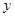 轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.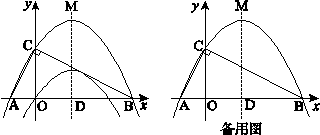
相关知识点
推荐套卷
已知二次函数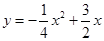 .
.(1)求它的对称轴与
 轴交点D的坐标;
轴交点D的坐标;(2)将该抛物线沿它的对称轴向上平移,如图所示,设平移后的抛物线的顶点为
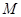 ,与
,与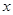 轴、
轴、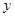 轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
轴的交点分别为A、B、C三点,连结AC、BC,若∠ACB=90°.
①求此时抛物线的解析式;
②以AB为直径作圆,试判断直线CM与此圆的位置关系,并说明理由.