古希腊著名的毕达哥拉斯学派把1，3，6，10 ，…这样的数称为“三角形数”（如图①），而把1，4，9，16，…这样的数称为“正方形数”（如图②）．如果规定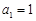
，
，
，
，…；
，
，
，
，…；
，
，
，
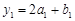，…，那么，按此规定，
，
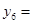＝ （用含n的式子表示，n为正整数）．
= ．
= ．
相关知识点
推荐套卷
古希腊著名的毕达哥拉斯学派把1，3，6，10 ，…这样的数称为“三角形数”（如图①），而把1，4，9，16，…这样的数称为“正方形数”（如图②）．如果规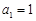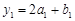定，，，，…；，，，，…；，，，，…，那么，按此规定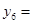， ，＝ （用含n的式子表示，n为正整数）．
粤公网安备 44130202000953号