已知：如图，在平面直角坐标系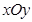
中，边长为
的等边
随着顶点A在抛物线
上运动而运动，且始终有BC∥x轴．
（1）当顶点A运动至与原点重合时，顶点C是否在该抛物线上？
（2）
在运动过程中有可能被x轴分成两部分，当上下两部分的面积之比为1∶8（即
）时，求顶点A的坐标；（3）
在运动过程中，当顶点B落在坐标轴上时，直接写出顶点C的坐标．
相关试题
（2）
，然后选取一个使原式有意义的
的值代入求值.
（2）
个单位每秒速度运动，运动时间为t．
相关知识点
推荐套卷
已知：如图，在平面直角坐标系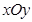中，边长为的等边随着顶点A在抛物线上运动而运动，且始终有BC∥x轴．（1）当顶点A运动至与原点重合时，顶点C是否在该抛物线上？
（2）
在运动过程中有可能被x轴分成两部分，当上下两部分的面积之比为1∶8（即）时，求顶点A的坐标；（3）
在运动过程中，当顶点B落在坐标轴上时，直接写出顶点C的坐标．
粤公网安备 44130202000953号