如下图是用棋子摆成的“T”字图案.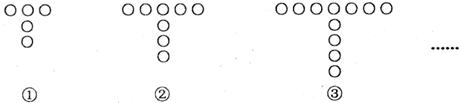
从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子.
(1)照此规律,摆成第八个图案需要几枚棋子?
(2)摆成第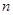 个图案需要几枚棋子?
个图案需要几枚棋子?
(3)摆成第2010个图案需要几枚棋子?
如下图是用棋子摆成的“T”字图案.
从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子.
(1)照此规律,摆成第八个图案需要几枚棋子?
(2)摆成第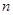 个图案需要几枚棋子?
个图案需要几枚棋子?
(3)摆成第2010个图案需要几枚棋子?