已知函数
.
(1)若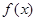
的部分图象如图所示，求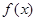的解析式;
(2)在(1)的条件下，求最小正实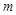数
，使得函数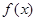的图象向左平移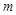个单位后所对应的函数是偶函数;
(3)若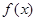在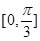
上是单调递增函数，求
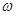的最大值.
，
的单调性；
是定义在
上的奇函数，当
，
，求
的最大值与最小值；
的最大值与最小值；
，
，
的值及
； 
，求
|
，
，求：
； （2）
相关知识点
推荐套卷
已知函数.
(1)若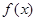的部分图象如图所示，求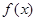的解析式;
(2)在(1)的条件下，求最小正实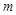数，使得函数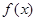的图象向左平移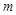个单位后所对应的函数是偶函数;
(3)若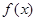在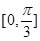上是单调递增函数，求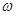的最大值.
粤公网安备 44130202000953号