（本小题满分14分）
现有甲，乙，丙，丁四名篮球运动员进行传球训练，由甲开始传球（即第一次传球是由甲传向乙或丙或丁），记第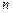
次传球球传回到甲的不同传球方式种数为
.
（1）试写出
,
并找出
与（
）的关系式；
（2）求数列
的通项公式；
（3）证明：当时, 
.
相关试题
为菱形，且
，
．
；
，求二面角
的余弦值。
．
，且
，求θ的值；
，且△ABC的面积为
，求sinA＋sinB的值．
满足
，且对任意
，都有
．
对任意
恒成立，求实数k的取值范围．
．
，试比较
与
的大小；
，且
在区间
上没有零点，求实数m的取值范围．推荐套卷
（本小题满分14分）
现有甲，乙，丙，丁四名篮球运动员进行传球训练，由甲开始传球（即第一次传球是由甲传向乙或丙或丁），记第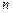次传球球传回到甲的不同传球方式种数为.
（1）试写出,并找出与（）的关系式；
（2）求数列的通项公式；
（3）证明：当时, .
粤公网安备 44130202000953号