如图,已知抛物线C1: 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点A的横坐标是
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点A的横坐标是 .
.
求
 点坐标及
点坐标及 的值;
的值;
如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向左平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点A成中心对称时,求C3的解析式
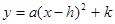 ;
;
如图(2),点Q是x轴负半轴上一动点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、E为顶点的三角形是直角三角形时,求顶点N的坐标.

相关知识点
推荐套卷
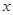 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回, 多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算 出
件合格品后,进行如下试验:随机抽取1件进行检测,然后放回, 多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算 出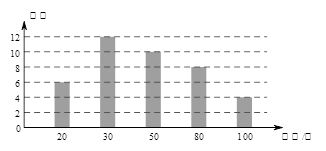
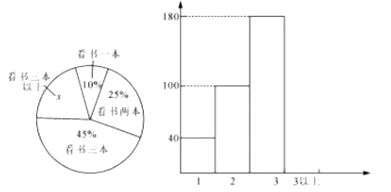
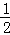 x刻画.
x刻画.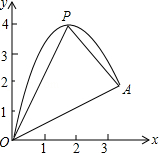
 粤公网安备 44130202000953号
粤公网安备 44130202000953号