阅读材料,数学家高斯在读书时曾经研究过这样一个问题: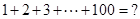
经过研究,这个问题的一般性结论是:
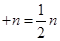
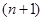 ,其中
,其中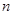 是正整数.
是正整数.
现在我们来研究一个类似的问题: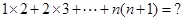
观察下面三个特殊的等式: 
将这三个等式的两边分别相加,可以得: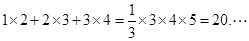
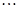
读完这段材料,请你思考后回答:
(1)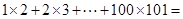 ___________________ ;
___________________ ;
(2)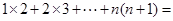 ______________________ ;
______________________ ;
(3) ___________ .
___________ .
相关知识点
推荐套卷
 与
与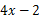 成正比例,且当
成正比例,且当 时,
时,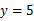 .
.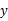 与
与 的函数关系式;
的函数关系式;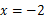 时的函数值.
时的函数值. 的图象与
的图象与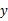 轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.
轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.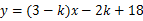 ,
, 为何值时,它的图象经过原点;
为何值时,它的图象经过原点; ).
).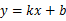 的图象经过点(
的图象经过点( ,
,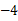 ),且与正比例函数
),且与正比例函数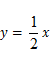 的图象相交于点(4,
的图象相交于点(4, ),
), 、
、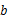 的值;
的值; 轴相交得到的三角形的面积.
轴相交得到的三角形的面积.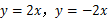 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号