如图，抛物线y=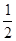
x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（-1，0）．⑴求抛物线的解析式及顶点D的坐标；
判断△ABC的形状，证明你的结论；
点M(m，0)是x
轴上的一个动点， 当CM+DM的值最小时，求m的值．
相关试题
的一元二次方程
有实数根，
为正整数.
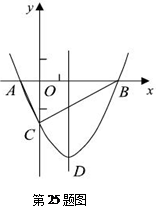
相关知识点
推荐套卷
如图，抛物线y=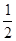x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（-1，0）．⑴求抛物线的解析式及顶点D的坐标；
判断△ABC的形状，证明你的结论；
点M(m，0)是x
轴上的一个动点， 当CM+DM的值最小时，求m的值．
粤公网安备 44130202000953号