数列{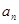 }的前n项和记为
}的前n项和记为 ,a1=t,
,a1=t, =2
=2 +1(n∈N+).
+1(n∈N+).
(Ⅰ)当t为何值时,数列{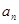 }是等比数列;
}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,若等差数列{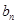 }的前n项和
}的前n项和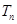 有最大值,且
有最大值,且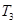 =15,又
=15,又
a1+b1,a2+b2,a3+b3成等比数列,求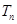 .
.
推荐套卷
数列{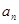 }的前n项和记为
}的前n项和记为 ,a1=t,
,a1=t, =2
=2 +1(n∈N+).
+1(n∈N+).
(Ⅰ)当t为何值时,数列{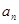 }是等比数列;
}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,若等差数列{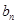 }的前n项和
}的前n项和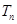 有最大值,且
有最大值,且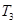 =15,又
=15,又
a1+b1,a2+b2,a3+b3成等比数列,求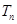 .
.