长虹网络蓝光电视机自投放市场以来，经过两次降价，单价由原来的20000元降到12800元。
（Ⅰ）求这种电视机平均每次降价的百分率，并写出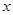
年后该电视的价格
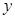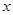与的函数关系式.
（Ⅱ）若按（1）中的平均降价百分率计算，问四年后该电视机的价格为多少元？
满足约束条件
，求目标函数
的最小值和最大值。
中，
求
的值。
（2）
及椭圆
,过点
的动直线与椭圆相交于
两点．
中点的横坐标是
，求直线
2）在
轴上是否存在点
，使
为常数？若存在，求出点
是公比大于1的等比数列，
为数列
项和．已知
，
构成等差数列．
，求数列
的前
．推荐套卷
长虹网络蓝光电视机自投放市场以来，经过两次降价，单价由原来的20000元降到12800元。
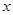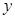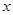（Ⅰ）求这种电视机平均每次降价的百分率，并写出年后该电视的价格与的函数关系式.
（Ⅱ）若按（1）中的平均降价百分率计算，问四年后该电视机的价格为多少元？
粤公网安备 44130202000953号