已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
某医院2014年3月份20名新生儿体重的频数分布表
某医院2014年3月份20名新生儿体重的频数分布表
|
组别(kg)
|
划记
|
频数
|
|
略
|
|
|
略
|
|
3.55-3.95
|
正一
|
6
|
|
略
|
|
|
略
|
|
|
略
|
|
合计
|
20
|
(1)求这组数据的极差;
(2)若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量(温馨提示:请在答题卷的对应位置填写,填写在试题卷上无效)
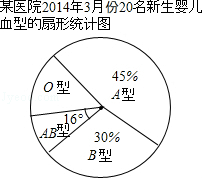
(3)经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求:
①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.