(本题7分)对于二次函数 ,如果当
,如果当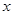 取任意整数时,
取任意整数时,
函数值 都是整数,此时称该点(
都是整数,此时称该点(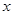 ,
, )为整点,该函数的图象为整点抛物线
)为整点,该函数的图象为整点抛物线
(例如: ).
).
(1)请你写出一个整点抛物线的解式 .(不必证明);
(2)请直接写出整点抛物线
 与直线
与直线 围成的阴影图形中
围成的阴影图形中
(不包括边界)所含的整点个数 .
相关知识点
推荐套卷
(本题7分)对于二次函数 ,如果当
,如果当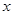 取任意整数时,
取任意整数时,
函数值 都是整数,此时称该点(
都是整数,此时称该点(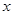 ,
, )为整点,该函数的图象为整点抛物线
)为整点,该函数的图象为整点抛物线
(例如: ).
).
(1)请你写出一个整点抛物线的解式 .(不必证明);
(2)请直接写出整点抛物线
 与直线
与直线 围成的阴影图形中
围成的阴影图形中
(不包括边界)所含的整点个数 .