台州市江南汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价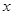 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为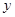 万元.(销售利润
万元.(销售利润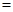 销售价
销售价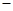 进货价)
进货价)(1)求
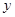 与
与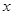 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出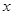 的取值范围;
的取值范围;(2)假设这种汽车平均每周的销售利润为
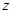 万元,试写出
万元,试写出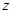 与
与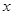 之间的函数关系式;
之间的函数关系式;(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
相关知识点
推荐套卷
 是否在直线
是否在直线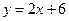 上时,常用的方法:把
上时,常用的方法:把 代入
代入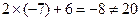 ,判断出点
,判断出点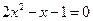 。
。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号