某区教育局为了了解学生参加阳光体育活动的情况，对某校学生进行随机抽样
调查，其中一个问题是“你平均每天参加阳光体育活动的时间是多少?”，共有4个选项：
A．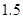
小时以上 B．
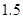～小时 C．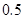
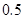～小时 D．小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图，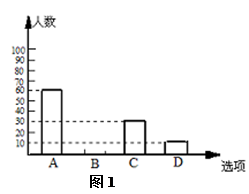
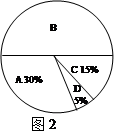
请你根据统计图提供的信息，解答以下问题：
(1)本次一共调查了多少名学生?
(2)在图
中将选项B的部分补充完整； (3)若该校有
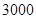名学生，你估计全校可能有多少名学
生平均每天参加体育活动的时间在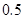小时以下．
相关试题
的大小．请你自编一道有理数混合运算题并解答，题目要求同时满足以下条件：
（1）必须含有加、减、乘、除、乘方5种运算；（2）除数必须是分数；（3）乘方运算中的底数必须是负分数；（4）计算结果等于2008。
，宽为
（
）；正方形铁皮的边长为
。现根据需要，要把两张铁皮
焊接成一张长方形的铁皮，新铁皮长
，请你求出新铁皮的宽。相关知识点
推荐套卷
粤公网安备 44130202000953号