佛山某学校的场室统一使用“佛山照明”的一种灯管，已知这种灯管使用寿命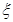
（单位：月）服从正态分布
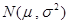，且使用寿命不少于
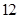个月的概率为
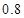，使用寿命不少于
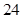个月的概率为
.
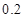（1）求这种灯管的平均使用寿命
；
（2）假设一间功能室一次性换上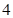
支这种新灯管，使用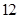个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.
相关试题
时，求函数
的单调递增区间；
，
，存在函数
，
，且点P使
，
，
成公差小于零的等差数列
，
为
，
的夹角，求
中，A．B．C的对边分别为
，
，
。且
，
的值
，
，求
，
的值域
的图像下有一系列正三角形，求第n个正三角形的边长.
相关知识点
推荐套卷
佛山某学校的场室统一使用“佛山照明”的一种灯管，已知这种灯管使用寿命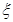（单位：月）服从正态分布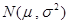，且使用寿命不少于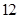个月的概率为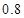，使用寿命不少于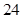个月的概率为.
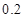（1）求这种灯管的平均使用寿命；
（2）假设一间功能室一次性换上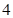支这种新灯管，使用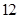个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.
粤公网安备 44130202000953号