设函数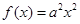 (
(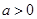 ),
),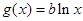 .
.
(1) 将函数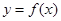 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数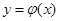 的图象,试写出
的图象,试写出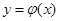 的解析式及值域;
的解析式及值域;
(2) 关于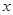 的不等式
的不等式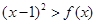 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数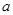 的取值范围;
的取值范围;
(3)对于函数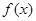 与
与 定义域上的任意实数
定义域上的任意实数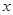 ,若存在常数
,若存在常数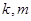 ,使得
,使得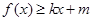 和
和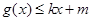 都成立,则称直线
都成立,则称直线 为函数
为函数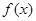 与
与 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究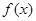 与
与 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
推荐套卷
设函数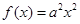 (
(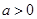 ),
),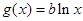 .
.
(1) 将函数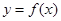 图象向右平移一个单位即可得到函数
图象向右平移一个单位即可得到函数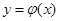 的图象,试写出
的图象,试写出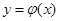 的解析式及值域;
的解析式及值域;
(2) 关于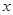 的不等式
的不等式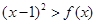 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数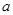 的取值范围;
的取值范围;
(3)对于函数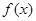 与
与 定义域上的任意实数
定义域上的任意实数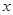 ,若存在常数
,若存在常数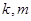 ,使得
,使得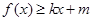 和
和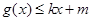 都成立,则称直线
都成立,则称直线 为函数
为函数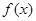 与
与 的“分界线”.设
的“分界线”.设 ,
, ,试探究
,试探究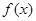 与
与 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.