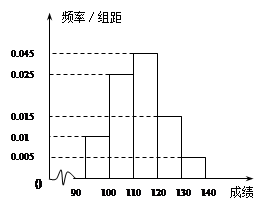某校高三数学竞赛考试后，对90分以上的成绩进行统计，其频率分布直方图如图所示、。若130～140分数段的人数为2人。
（1）请估计一下这组数据的平均数M；
（2）现根据初赛成绩从第一组和第五组（从低分段到高分段依次为第一组、第二组、…、第五组）中任意选出两人，形成帮扶小组。若选出的两人成绩差大于20，则称这两人为“黄金搭档组”，试求选出的两人为“黄金搭档组”的概率。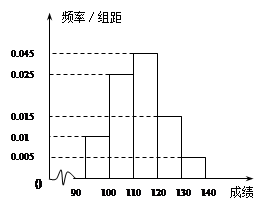
相关试题
，
.
为等比数列；
，其中
为常数，且
，
，求
.
满足：
，定义域为
的函数
，不等式
恒成立，求实数
的取值范围。
的最大值为
，
，与
轴的交点坐标为
. 
，
为其前
项和，求
.
中的内角
，
，
所对的边长分别为
，
，
，且
,
.
时，求角
的定义域为集合A,集合 B={
＜0}．
时，求A
B； 
A的实数
的取值范围。推荐套卷
某校高三数学竞赛考试后，对90分以上的成绩进行统计，其频率分布直方图如图所示、。若130～140分数段的人数为2人。
（1）请估计一下这组数据的平均数M；
（2）现根据初赛成绩从第一组和第五组（从低分段到高分段依次为第一组、第二组、…、第五组）中任意选出两人，形成帮扶小组。若选出的两人成绩差大于20，则称这两人为“黄金搭档组”，试求选出的两人为“黄金搭档组”的概率。
粤公网安备 44130202000953号