已知抛物线 的焦点为F,椭圆C:
的焦点为F,椭圆C: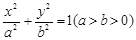 的离心率为
的离心率为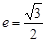 ,
,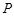 是它们的一个交点,且
是它们的一个交点,且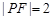 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知 ,点A,B为椭圆
,点A,B为椭圆 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴,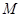 是
是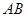 的中点,试探究
的中点,试探究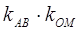 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。
相关知识点
推荐套卷
已知抛物线 的焦点为F,椭圆C:
的焦点为F,椭圆C: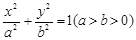 的离心率为
的离心率为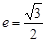 ,
,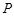 是它们的一个交点,且
是它们的一个交点,且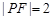 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知 ,点A,B为椭圆
,点A,B为椭圆 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴,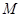 是
是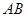 的中点,试探究
的中点,试探究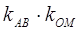 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。