(本题15分)已知曲线 与曲线
与曲线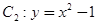 ,设点
,设点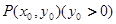 是曲线
是曲线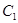 上任意一点,直线
上任意一点,直线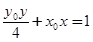 与曲线
与曲线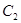 交于
交于 、
、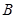 两点.
两点.
(1)判断直线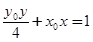 与曲线
与曲线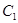 的位置关系;
的位置关系;
(2)以 、
、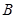 两点为切点分别作曲线
两点为切点分别作曲线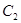 的切线,设两切线的交点为
的切线,设两切线的交点为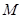 ,求证:点
,求证:点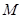 到直线
到直线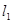 :
: 与
与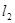 :
: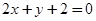 距离的乘积为定值.
距离的乘积为定值.
推荐套卷
(本题15分)已知曲线 与曲线
与曲线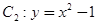 ,设点
,设点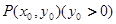 是曲线
是曲线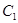 上任意一点,直线
上任意一点,直线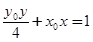 与曲线
与曲线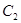 交于
交于 、
、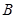 两点.
两点.
(1)判断直线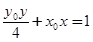 与曲线
与曲线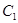 的位置关系;
的位置关系;
(2)以 、
、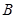 两点为切点分别作曲线
两点为切点分别作曲线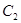 的切线,设两切线的交点为
的切线,设两切线的交点为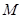 ,求证:点
,求证:点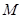 到直线
到直线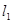 :
: 与
与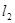 :
: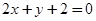 距离的乘积为定值.
距离的乘积为定值.