本题满分14分) 设函数f (x)＝ln x＋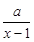
在(0，
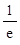) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1，＋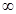
)．求证：f (x2)－f (x1)＞e＋2－．
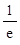注：e是自然对数的底数．
相关试题
的前
项和为
，数列
是首项为
，公差为
（
）的等差数列，且
，
，
成等比数列．
（
），求数列
的前
．
（
）的导函数
，数列
的前
项和为
，点
（
）均在函数
的图象上．
，
，
．
的值；
，
，且
，求
的值．
、
、
分别为
的三边
、
、
所对的角，向量
，
，且
．
，
，
成等差数列，且
，求边
（
）．
时，求函数
的单调区间；
，当
时，函数
的最大值为
，求
的取值范围．推荐套卷
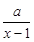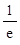本题满分14分) 设函数f (x)＝ln x＋在(0，) 内有极值．
(Ⅰ) 求实数a的取值范围；
(Ⅱ) 若x1∈(0，1)，x2∈(1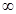，＋)．求证：f (x2)－f (x1)＞e＋2－．
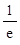注：e是自然对数的底数．
粤公网安备 44130202000953号