（已知抛物线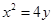
，过定点
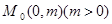的直线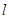
交抛物线于A、B两点.
（Ⅰ）分别过A、B作抛物线的两条切线，A、B为切点，求证：这两条切线的交点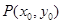
在定直线
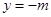上.
（Ⅱ）当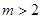
时，在抛物线上存在不同的两点P、Q关于直线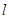对称，弦长|PQ|中是否存在最大值？若存在，求其最大值（用
表示），若不存在，请说明理由.
是等差数列，且
，
．
项和
；
的值．
且周长为6，
成等比数列，求(1)△ABC的面积S的最大值； (2)
的取值范围.
，求
的其他三角函数值．
，
且
，
的简图．
，当它的半径和圆心角各取什么值时，才能使扇形的面积最大？最大面积是多少？相关知识点
推荐套卷
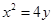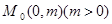（已知抛物线，过定点的直线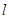交抛物线于A、B两点.
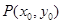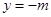（Ⅰ）分别过A、B作抛物线的两条切线，A、B为切点，求证：这两条切线的交点在定直线上.
（Ⅱ）当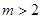时，在抛物线上存在不同的两点P、Q关于直线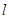对称，弦长|PQ|中是否存在最大值？若存在，求其最大值（用表示），若不存在，请说明理由.
粤公网安备 44130202000953号