．(本小题满分14分)设抛物线
的方程为
，
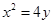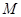为直线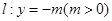
上任意一点，过点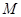作抛物线的两条切线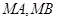
，切点分别为
,
.
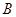（1）当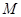的坐标为
时，求过
三点的圆的方程，并判断直线
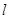与此圆的位置关系；
（2）求证：直线
恒过定点；
（3）当
变化时，试探究直线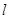上是否存在点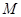，使
为直角三角形，若存在，有几个这样的点，若不存在，说明理由.
<
，求实数m的取值范围.
的草图，并求出其单调区间.
的大小.
+
):相关知识点
推荐套卷
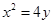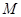．(本小题满分14分)设抛物线的方程为，为直线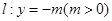上任意一点，过点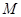作抛物线的两条切线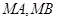，切点分别为,.
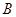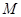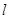（1）当的坐标为时，求过三点的圆的方程，并判断直线与此圆的位置关系；
（2）求证：直线恒过定点；
（3）当变化时，试探究直线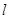上是否存在点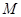，使为直角三角形，若存在，有几个这样的点，若不存在，说明理由.
粤公网安备 44130202000953号